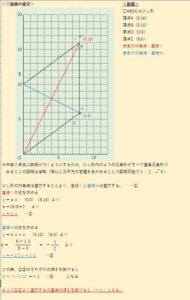
三角形の面積を求める公式の考え方 @城陽市寺田にある個別指導塾 勉楽個別 寺田小・寺田西小・寺田南小・今池小・富野小・深谷小・久世小・久津川小・古川小・城陽中・西城陽中・東城陽・北城陽中・南城陽中・南陽高・城南菱創高・莵道高・久御山高・城陽高
みなさん、こんばんは。
京都府城陽市寺田にある個別指導勉楽個別です。
本日もブログを読んでくださりありがとうございます。
本日のブログは、「理解して覚えることの重要性」を三角形の面積を求める公式を基にして書こうと思います。
理解して覚えることの重要性
みなさんは、「公式を覚える勉強」をしていませんか?
勿論、公式を覚えることは重要です。
しかし、「訳も分からず覚えること」はあまり意味がありません。
重要なことは「何故そうなるのかを理解して覚えること」なのです。
その上で「公式を覚えること」はとても意味があります。
そして、覚えやすく、忘れにくく、思い出しやすくなるのです。
正方形を用いた三角形の面積の公式
先ず、画像を見てください。
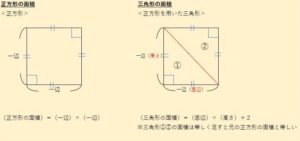
小学校では、3年生で正方形・長方形の面積を学習します。
そして、4年生で三角形の面積を学習します。
当然、これにもきちんと理由がある訳です。
先ず、正方形の面積を求める公式です。
(正方形の面積)=(一辺)×(一辺)
画像にも書かれている通りですね。
次に、三角形の面積を求める公式です。
この場合、正方形の一辺を「底辺」と「高さ」に置き換えます。
この時に大切なことは、三角形の「底辺」と「高さ」の関係です。
三角形の底辺と高さは「直交(垂直に交わる)」しますが、正方形や長方形の場合は「4つの角が全て直角」です。
なので、これらを基にして考える訳ですね。
次に、右の図のように対角線(赤色)で正方形を2つに分けて三角形を2つ作ります。
また、この時、この2つの三角形は同じ形(合同)になります。
つまり、この時の三角形の面積は「正方形の面積を二等分したもの」になるのです。
なので、三角形の面積を求める公式は次のようになるのです。
(三角形の面積)=(底辺)×(高さ)÷2
※底辺・高さともに「一辺」の長さと等しい
おまけ
また、「三角形の底辺と高さは直交する」ことを正しく理解しておくと、「高さ」がどの部分になるかを間違わないのです。
因みに、私が三角形の「高さ」の説明する時は次のように説明します。
「三角形の高さは、底辺の向かい側になる頂点から底辺に向けて引いた垂線のこと」
流石に小学生にはこの説明はしませんが、中学生にはこのように説明します。
その理由は、「用語を正しく理解し覚えて欲しいから」です。
言い換えると、「何となく理解し、何となく覚え、何となく出来たり間違ったりする」ことを避けたいからです。
因みに、「底辺」て1つじゃないんですが、みなさん大丈夫ですよね。
三角形の三辺すべてが「底辺」として考えられます。
そして、その1つ1つの底辺には「1つ1つに適応したそれぞれの高さがある」のです。
また、「台形」の面積を求める公式を思い出してください。
(上底+下底)×高さ÷2ですよね。
この「上底」って「上底辺」のことなのです。
ということは、、、ですよね!
是非、みなさんも「何となく」ではなく「1つ1つ正しく理する勉強」に取り組んでくれると嬉しいです。