みなさん、こんにちは。

 

京都府城陽市寺田にある個別指導勉楽個別です。

 

本日もブログを読んでくださりありがとうございます。

 

本日のブログは「勉強の仕方」についての内容です。

 

しかし、画像や内容は「目の前の1問の解き方」です。

 

「あれっ？」という感じですが、進めてみましょう。

 

生徒諸君の勉強の仕方

 

先ずは、画像の問題と解き方を確認してください。

 

 

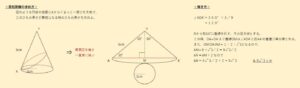
公立高校の入試問題にもよく出る問題です。

 

しかし、同じ問題が「中学入試」でも出題されたりします。

 

少し脱線します。

 

また、その時には母線と底面の円の半径の長さのバランスが違うことが多いです。

 

例えば、「母線＝１２ｃｍ、底面の円の半径＝２ｃｍ」という感じです。

 

その上で、解き方は同じ方法で解くことが出来るのです。

 

話を元に戻します。

 

中学生のみなさんがこの問題を解く時や分からなくて解説を見て勉強する時、意識は何に向いていますか？

 

多分、「展開図を見てどう解くのかを追っている」のではないでしょうか。

 

次の画像の問題も同じです。

 

 

勉強の重要なポイント

 

どちらの問題も「赤文字」で書いてある「上2行」は同じ内容です。

 

お気付きでしたか？

 

要するに、「立体の紐かけ最短距離の問題」の解き方で最初にやることは1つなのです。

 

「展開図を描いて、始点と終点を一直線に結ぶ」ことなのです。

 

その後は、必要な知識や解法が身に付いているかどうかです。

 

しかし、最初にやるべき「展開図を描く」ことを中学生諸君はあまり練習していないのではないでしょうか？

 

先に書いた「中学受験にも出題される」ということは、小学生でも解くことが可能です。

 

そして、中学受験をする小学生達は「展開図を描くこと」は嫌というほど取り組みます。

 

また、いくつか書かれたサイコロの展開図で「正しいものを選ぶ」ような「逆展開図」の取り組みもしています。

 

だから「中学受験を経験した子ども達」は出来る問題の範囲が広いことが多いのです。

 

因みに、中学3年生で学ぶ「三平方の定理」の三角定規のパターンの一部は小学生も利用することが出来ます。

 

例えば、「３０°、６０°、９０°」の細長い三角定規です。

 

その最も短い辺と斜辺の比が「１：２」であることを利用するのです。

 

ショートカットしないこと

 

中学受験を目指す小学生達は、きちんと基礎基本の理解と必要な作図力や知識の習得に取り組みます。

 

しかし、中学生になると何故かその部分を軽視します。

 

そして、その理解や習得をしていないまま「お試し演習」をするのです。

 

「お試し演習」とは、「先ずは問題を解いてみて間違った問題だけを勉強するために行う演習のこと」です。

 

これをやってしまうと、「再現性の範囲」が狭まります。

 

どういうことかというと、「理論や仕組みが正しく理解出来ていないまま」何となく解いて何となく正解し、何となく間違ってしまうのです。

 

「そんなことありえない」と思われるかもしれませんが、現場では普通にあることです。

 

違う言い方をすると、「問題を解けさえすれば良い」と考えているのです。

 

だから、「面倒な基礎基本の理解や地道な努力」を省いてしまうのです。

 

期末テストも2週間後に迫りましたので、しっかりと正しく勉強に取り組んでくださいね。