大切なのは質か量か @城陽市寺田にある個別指導塾 勉楽個別 寺田小・寺田西小・寺田南小・今池小・富野小・深谷小・久世小・久津川小・古川小・城陽中・西城陽中・東城陽・北城陽中・南城陽中・南陽高・城南菱創高・莵道高・久御山高・城陽高
みなさん、こんにちは。
京都府城陽市寺田にある個別指導勉楽個別です。
本日もブログを読んでくださりありがとうございます。
大切なのは質か量か
結論から言うと、「良い質の物を、たくさんの量取り組むこと」でしょう。
例えば、中学受験指導をしている我々「塾人」を例にしてみます。
最難関中学校の1つである灘中学の算数の問題は、プロ講師でも簡単に解くことは出来ません。
自分の中にある知識や過去に取り組んだ解法をいくつも組み合わせます。
そして、解くことが出来なかった方法を消し込みながら解き進めるのです。
その場合、一発で解けることもあれば、何度も解き直しをしなければならないこともあります。
また、問題中に与えられた図も「全くバランスが違う図」が与えられることもしばしばです。
今年の長方形と三角形が組み合わさった問題もそうでした。
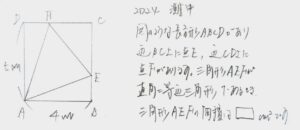
一見簡単そうで解けそうな問題です。
しかし、△AEFのどの角が直角なのかを特定する必要もあります。
その上、「このままの図」では非常に分かりにくく間違いやすいのです。
因みに、答えは「8.5cm²」となります。
前提として大切なこと
難問を解こうとすると、どうしても「応用発展系の知識」を学ぼうとします。
しかし、その前に「基礎基本」が備わっていないと意味がありません。
因みに、「備わっている」というのは「知っているだけでなく使いこなせる状態」です。
先の問題でも、先ずはもう少し「それらしい図に書き直す」と良いでしょう。
そして、分かる角度や関係性を図示し、1つ1つ「分かっていることと分からないことを明らかにする」のです。
そして、そこからが「テクニックの出番」です。
中学受験算数の図形問題では、いくつかの重要テクニックがあります。
「三角定規の直角三角形を見つける・作り出す」
「同じ図形をくっ付けてみる」
「欠けている部分を補って正方形を作る」
等が、その中でも基本テクニックです。
そして、これらを「いつでも使いこなせるようにする」には「量や回数」が必要になります。
そうしないと、「1回出来た程度では、直ぐに出来なくなってしまう」のです。
全く話は変わりますが、ここ数日でたくさんの御礼の品や過去の卒塾生からお土産を頂戴しています。
お電話で御礼をお伝えしていますが、この場でも御礼申し上げます。





